Argumentation Solvers

This page describes a series of argumentation solvers that can be used in the computation of solutions to decision and enumeration problems under several argumentation semantics.

totle is the latest version of what were earlier known as GRIS and then EqArgSolver.

GRIS used the Gabbay-Rodrigues Iteration Schema starting from a particular configuration of initial values to do some operations needed in the computation of argumentation semantics. GRIS is essentially numeric and has applications beyond the 3-valued semantics. A light-touch spin-off of GRIS, showing just the evolution of the numerical values through the iteration schema is available here.

EqArgSolver then limited the use of the equation schema, eventually opting instead for a more sophisticated, custom-made algorithm optimised for 3-valued semantics only. EqArgSolver was last submitted to the 2019 ICCMA competition and binaries are still available from here

totle is implemented in C++ and incorporates a number of improvements over EqArgSolver, e.g., better memory management, optimisations of the original alogirthm, and support for a new parallel algorithm for computation of extensions (in development).

Given an argumentation framework <S,R>, totle can be used to compute one or all of the extensions of the framework under the grounded, complete, preferred and stable semantics as well as to decide whether an argument X of S is accepted in one or all of the extensions under one of these four semantics.

Argumentation problems must be submitted to totle using probo's syntax (whose basic usage can be found here). The input argumentation framework must be supplied as a file in the trivial graph format (TGF), which is basically a text file containing a sequence of node designators one per line, followed by the separator “#” in its own line, and then followed by a list of pairs of nodes, a pair per line, where the first element of each pair is the source of an edge in the graph (the attacker) and the second element is its target (the node being attacked).

Basic usage

totle must be invoked from the command line. In Windows, run a terminal window by right-clicking “Start” then typing “cmd” and then invoking totle as detailed below. For linux, simply type totle in any terminal window.

Running totle

<command> -f <inputfile> -p <problem> -fo tgf [-a <argumenttocheck>]

where command is one of totle (linux 64-bit); totle32.exe (Windows 32-bit); or totle64.exe (Windows 64-bit); inputfile is an input file in the TGF file format; and problem is one of

SE-σ: compute one extension under semantics σ
EE-σ: compute all extensions under semantics σ
DC-σ: decide whether argumenttocheck is accepted in some extension under semantics σ (decide credulously)
DS-σ: decide whether argumenttocheck is accepted in all extensions under semantics σ (decide skeptically)

Valid values for σ are: GR (grounded), CO (complete), PR (preferred) and ST (stable). For single extension semantics, such as the grounded semantics, only SE-GR and DC-GR are available.

For example, consider the argumentation framework of Figure 6.2 (taken from “Efficient Computation of Argumentation Semantics”, by Beishui Liao, page 72):

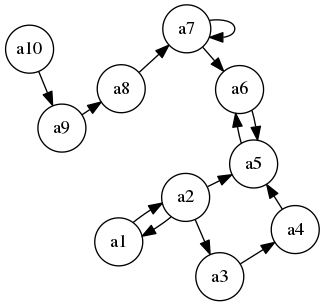
Its TGF representation is as follows (click here to download this file):


a1
a2
a3
a4
a5
a6
a7
a8
a9
a10
#
a1 a2
a2 a1
a2 a5
a2 a3
a3 a4
a4 a5
a5 a6
a6 a5
a7 a6
a7 a7
a8 a7
a9 a8
a10 a9

To calculate all preferred extensions of this framework, invoke totle as follows (linux version assumed):

./totle -f f6.2.tgf -fo tgf -p EE-PR

totle will return
[[a10,a2,a4,a6,a8],[a1,a10,a3,a6,a8],[a1,a10,a3,a5,a8]] indicating that the sets with arguments [a10,a2,a4,a6,a8]; and [a1,a10,a3,a6,a8]; and [a1,a10,a3,a5,a8] correspond to all the preferred extensions of this framework.

Similarly, notice that a10 is accepted in all preferred extensions; a2 is accepted in one of the preferred extensions but not all; and a9 is not accepted in any preferred extenstions. Therefore, the following invokations of totle would produce the corresponding results below.

`-a`	-p DC-PR	-p DS-PR
`a10`	`Yes`	`Yes`
`a2`	`Yes`	`No`
`a9`	`No`	`No`

Limitations

totle is not currently able to handle very large problems in the preferred semantics. By large we mean a framework with a large number of nodes in a single SCC, or a framework with a large number of non-trivial SCCs, or a combination of these, especially if these SCCs appear close to a source node in the framework induced by the SCCs. totle has successfully run is less complex frameworks with up to 2,500,000 arguments.

The two papers below describe totle in some detail, although improvements are regularly made to the solver.

Downloading totle

totle was last submitted to the 3rd International Competition on Computational Models of Argumentation, skipping the 4th ICCMA in 2021, due to a major re-development effort.
Its latest version incorporates several new developments and efficiency improvements but it's not available for general distribution. In the meantime, please feel free to request me a copy by e-mailing odinaldo.rodrigues@kcl.ac.uk.

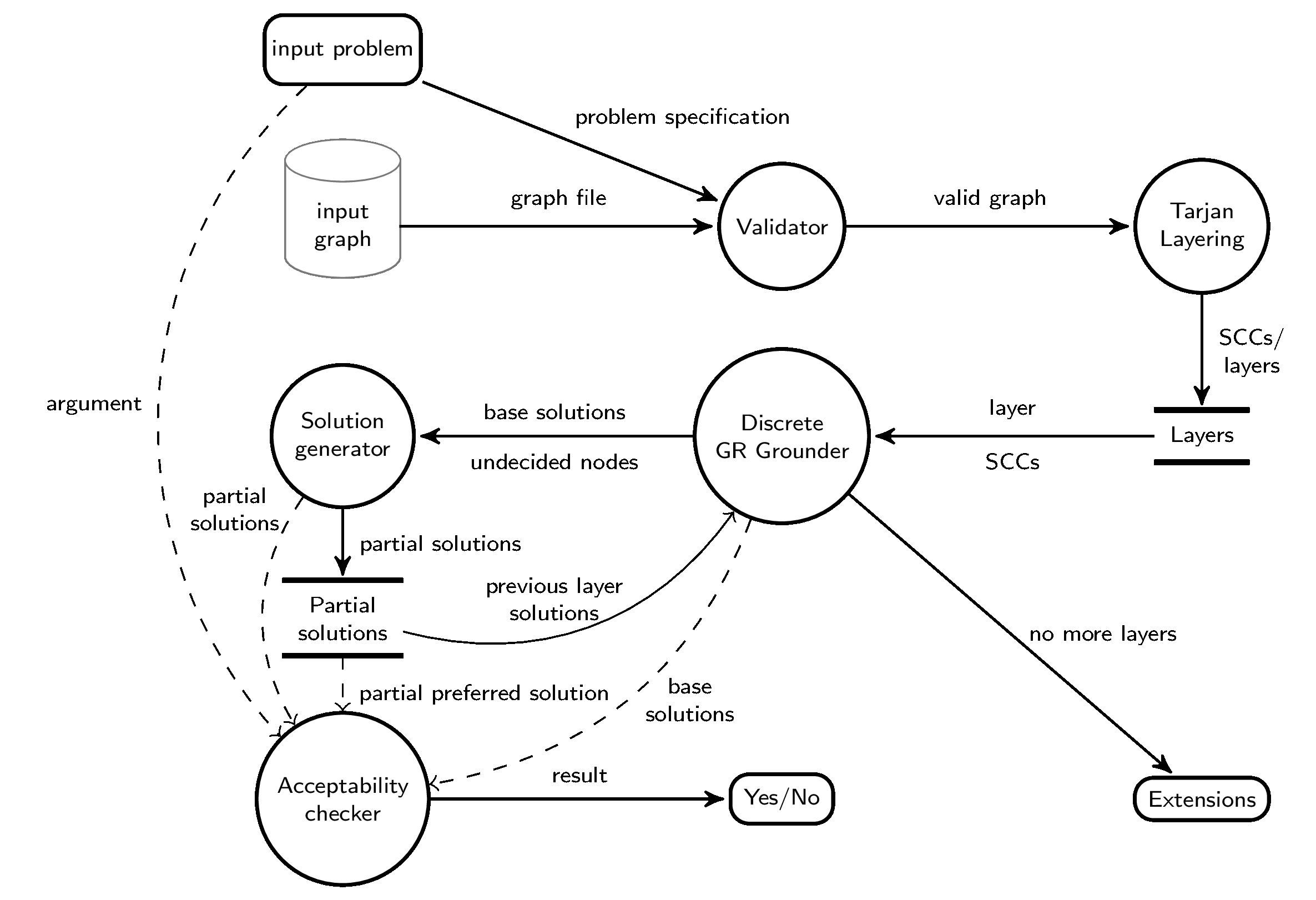
System description

totle works as described in the picture below.

Development path

totle is used as a laboratory for experimentation with algorithms for argumentation reasoning and as such is continually being updated.

The latest version uses an improved version of the algorithm described here, fixes some bugs, and is more efficient than the version submitted to the ICCMA 2019 competition, and includes some general improvements in performance.