The Gabbay-Rodrigues Iteration Schema
The Gabbay-Rodrigues Iteration Schema is a schema that computes values iteratively for a numerical argumentation framework based on initial values given to the framework's arguments.
The schema is given by the following equation, where Vi is the value of the argument X at iteration i (0 is the first iteration) and Att(X) are the attackers of the argument X:
The Gabbay-Rodrigues schema corrects the
initial values of the arguments, such that
in the limit of the sequence, we end
up with an extension (in Dung's sense) using the following
correspondence between the values of an argument X values and its label:
- V(X)=1 iff X=in (accepted)
- 0≤ V(X) ≤ 1 iff X=und (undecided)
- v(X)=0 iff X=out (defeated)
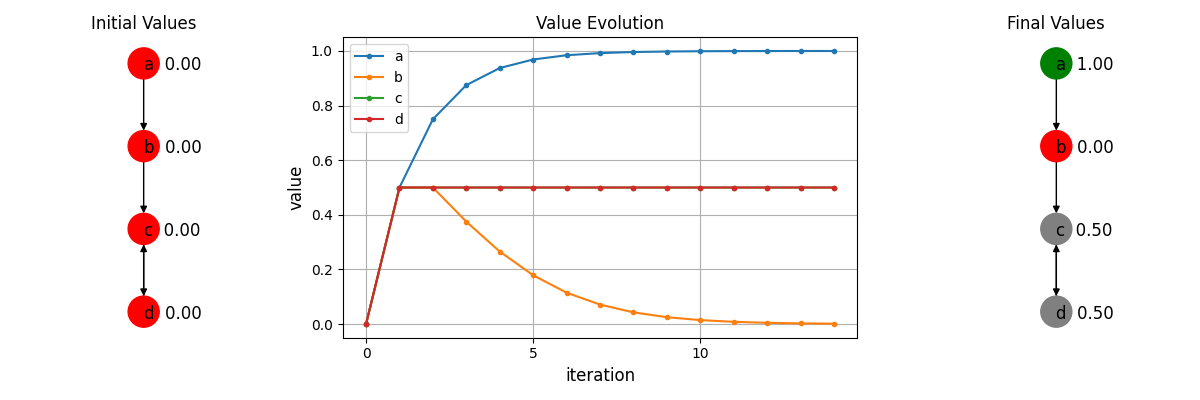
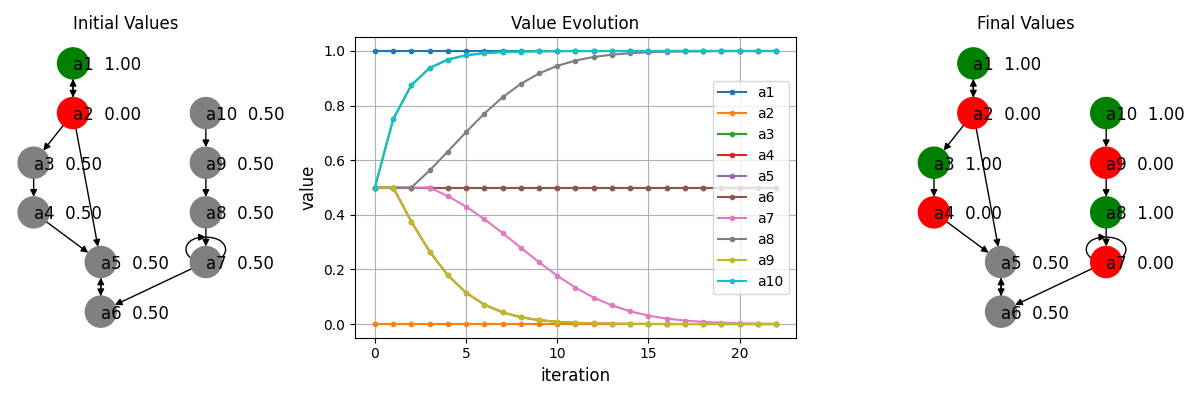
If the initial values already form an extension, the sequence will immediately stabilise and the final values will be the initial values. If the initial values do not correspond to an extension, the schema will correct the values and the extension we end up with depends on the initial values given. The paper explains in detail the relationship between the final extension and the admissible sets of the corresponding initial values.
A simple python script gris.py implementing the schema can be downloaded from the github repository here. The script takes as an argument an "augmented" TGF file whose arguments are provided with their initial numerical value. For example, the first argumentation framework below is specified with the TGF file:
a 0.5
b 0.5
c 0.5
d 0.5
#
a b
b a
b d
c d
The script will calculate the values in the sequence, stopping when a certain threshold is met (see python code for details).
Basic usage
gris must be invoked from the command line using python. For example:
python3 gris.py [example.tgf]
Below you can find some examples produced by gris.py, with initial and (approximated) final values:
Downloading gris.py
Get it from my github repository: https://github.com/odinaldo/gris