

Next: Writing up and presenting
Up: Research Methods
Previous: Accessing research literature
Subsections
Tools for doing research
Even for a project of only a few months it's useful to keep systematic notes of
your work: you'd be surprised how easy it is to forget within a couple
of months what you did at the beginning. Date your hand-written notes
and put them in a folder, in a logical order; if necessary, split them
into sections. It can also be useful to keep a simple electronic log
file (on your computer, or dropbox, or google docs etc), where you can record in ``bullet point style'' e.g.
- questions for your supervisor(s) for next time you meet
- observations from papers you've read, and which you'd like to
put into the project report
- results you've obtained and important ideas that should go into
the report
Such a log file can be a starting point for writing up the project
report; if you update it regularly, it'll ensure that you don't leave
out anything important. Again, it's surprising how easily this
happens, especially with results from the early stages of a
project. E.g. if you have to tune the parameters of a learning
algorithm, you should explain in the report how you did this; if you
don't have a record of which values you tried and what happened, this
will be very difficult.
Most project involve computation of some kind or other; you may need
to evaluate numerically the predictions of a theoretical calculation,
run some learning algorithms on data etc.
All M.Sc. students have access to the student computing facilities
around campus. There are also dedicated PCs in room S4.25; for
access to this room please contact the departmental
office in room S5.17.
You should try out early on
that you can log in to whatever College computer you are planning to use; if
there is a problem, send an email to
nms-computing-support@kcl.ac.uk
in the
first instance. The default printer for the PCs in S4.25 is in room S4.24;
again, ask in the departmental office for keys. Also check with them
regarding access on weekends etc; don't just assume you'll be able to
get into the rooms somehow, especially during the mad rush in the last
few days of the project period.
For heavier computation we can also give you access to our network of
Unix workstations. Your supervisor will be able to judge whether
this is necessary.
Exactly what software you'll need will depend on your project. For
simple calculations, spreadsheets may be enough; most machines have
openoffice (or staroffice) installed, which provide Microsoft
Excel-compatible spreadsheets.
For symbolic calculations, e.g. when you need to simplify a very
complicated expression, Maple and Mathematica are both
useful; Maple is available on most machines, as is Mathematica. These programs are also useful for making
graphs, and for not-too-complicated numerical work, e.g. minimizing
functions numerically, solving systems of nonlinear equations.
For complicated numerical work you may need to write your own
programmes. Standard languages in use in the department are C and C++,
and compilers (gcc) and debuggers (gdb) for these are on all Unix
workstations.
Finally, there is matlab. This is installed on the M.Sc. PCs (in room S4.25), but you can also install it on your own machine using a college licence. See here
for details.
Originally, matlab (matrix laboratory) was designed as a simple
interface for doing matrix and linear algebra computations. It retains
that structure, but lots of other functions have been added. One
reason that matlab is so popular is that it can easily be extended
using so-called toolboxes. Many of these are written by people doing
research in complex systems, and are freely available. Installed on
the machines in the MSc computer room should be for example the
netlab
neural networks
toolbox and the
OSUSVM
support
vector machine toolbox. The commercial toolboxes (produced by MathWorks,
the company that makes Matlab) for optimization and statistics are also there.
Because matlab is widely used and often features as a tool in M.Sc.
research projects, you are
strongly encouraged to familiarize yourself with it. Below is a short
overview; good tutorials can be found e.g. in the online Matlab help facility.
You could also have a look at these documents with
overviews of basic Matlab functions (document 1
(Word), document 2 (Word),
document 3 (pdf)), from previous modules within NMS.
Below is a brief summary of some features of matlab:
- Getting help: help <command> gives help on a particular
command; lookfor <topic> finds all commands whose name or
description includes the string <topic>.
- The basic objects are matrices, e.g. x = [1 2 3;4 5 6]
defines a matrix x with 2 rows and 3 columns with the given
entries. Ending a line with a ; suppresses the output. (Note the
difference: maple uses := for assignments, produces output
for lines ending in ; and is silent for lines ending in :).
- There are some preset operations for common matrices; e.g.
y=zeros(size(x)) will give you a matrix y of the same size as
x but with all entries 0. ones works in the same way.
- Matrices are thought as lists of their columns; x(1,3) and
x(5) both give output 3. Many operations act by default on
columns, e.g. sum(x) gives 5 7 9; mean and std
give means and standard deviations for each column. You can get row
operations by transposing (and complex conjugating) with ',
e.g. mean(x') gives 2 5.
- Ranges are indicated with colons. E.g. x = [1:5;3:2:12]
gives a matrix with first row 1 2 3 4 5 and second row 3 5
7 9 11.
- Ranges can be used to select submatrices. E.g. x(1,2:4)
gives elements 2 trough 4 of the first row of x. A colon on its
own gives the whole range, so that x(:,3:5) gives the last three
columns of x. There are also more complicated ways of selecting
only entries of x that obey certain conditions; this is called
``logical indexing''.
- Matrices can be added, subtracted and multiplied as usual;
^ gives powers. A division operator also exists:
x=A
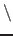 b gives
the solution of
b gives
the solution of 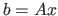 , and x=b/A gives the solution of
, and x=b/A gives the solution of 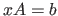 ;
note that in the second case both x and b are row vectors.
;
note that in the second case both x and b are row vectors.
- By default, operations are understood as matrix operations;
elementwise operations have a . before them. E.g. x=[1 2],
b=[2 3], y=x.
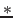 b gives 2 6. The operators
b gives 2 6. The operators 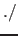 and
.^ similarly give elementwise division and power. Predefined
mathematical functions such as sin and exp are also
applied elementwise.
and
.^ similarly give elementwise division and power. Predefined
mathematical functions such as sin and exp are also
applied elementwise.
- Plots can be made by e.g. defining the x-range and then
applying an elementwise transformation, as in x=[0:0.05:7];
y=0.1
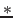 x.
x.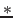 x+sin(x); plot(x,y). Note the semicolons here:
both x and y are rather long vectors which would clutter
the screen.
x+sin(x); plot(x,y). Note the semicolons here:
both x and y are rather long vectors which would clutter
the screen.
- 3d plots work similarly; try e.g.
[x,y]=meshgrid(0:0.05:1,-1:0.1:1); z = x.
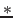 exp(-x.^2-y.^2); plot3(x,y,z). The meshgrid here
command defines two matrices x and y containing
respectively the
exp(-x.^2-y.^2); plot3(x,y,z). The meshgrid here
command defines two matrices x and y containing
respectively the 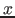 - and
- and 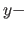 components of the grid of
points. Replacing plot3 by mesh has the obvious
effect. There are many other options for plots, including combining
subplots into one big plot etc.
components of the grid of
points. Replacing plot3 by mesh has the obvious
effect. There are many other options for plots, including combining
subplots into one big plot etc.
- The obvious mode of using matlab is by issuing commands from the
command line prompt: you can recall earlier commands with cursor keys
and edit them; typing the beginning of an earlier line will give you
just the matching lines. If you can't recall what variables you've
defined so far, use who; whos gives you more detailed
information.
- The alternative is to save commands in so-called ``m-files'':
saving a sequence of commands in dooda.m and then typing
dooda at the command prompt will execute those commands as if you'd
typed them in there and then. If you think you may want to make the
commands you're typing into a script, you can switch on a ``diary''
record of everything on the screen by typing diary on
<filename>; this saves everything until you issue the command
diary off.
- Going beyond scripts, you can define new matlab functions in
m-files. Here's an example:
function c = mygcd(a,b)
% mygcd(a,b) finds greatest common divisor of a and b
% no careful error checking so far; not sure what happens for
% non-integer input
% set c equal to the minimum of a and b; a shorter way would be
% c=min(a,b) but this version illustrates the use of conditional
% statements
c=a;
if(b<=a) c=b;
end
% decrease c as long as it's not a divisor of either a or b
while(mod(a,c)~=0 | mod(b,c)~=0)
c=c-1;
end
If you save this as a file mygcd.m and then type mygcd(25,10)
you'll get the greatest common divisor of 25 and 10 as the answer,
i.e. 5. You may need to change to the directory where you've saved
the m-file to get this to work; you can use the ``set path'' menu
item for this, or use e.g. cd  /Documents/.
/Documents/.
You'll notice that in m-files you can use loops and conditional
statements, just like in other programming languages. Defining a
function in an m-file also makes it accessible to help; e.g.
help mygcd displays the comment lines at the beginning of
mygcd.m. Functions can also have several variables as output, not just
a single number or vector.
- Since you can call one function from another, you can write
complete programs in terms of m-files. The m-file structure naturally
encourages you to make things modular. Matlab automatically handles
most of the work involved in defining and allocating local variables
automatically.
- The toolboxes are basically lots of m-files with useful
functions. help stats will show you all the functions in the
statistics toolbox, for example. Most toolboxes
come with demos: try e.g. disttool which is a graphical
interface for exploring probability distributions. polytool from the statistics
toolbox (see help stats) does polynomial fitting. Let's conclude
our foray into matlab with an illustration of over-fitting: Try
x=[-1:0.1:1]
sigma=0.1
y=x.^3-x+sigma*(rand(1,length(x))-0.5)
polytool(x,y,2)
The third argument of polytool specifies the degree of the
polynomial to be fitted initially; you can change this in the pop-up
window. You'll see that the data in y are a noisy version of
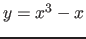 ; rand generates a vector of random variables, all
uniformly distributed between 0 and 1. You'll see that degree 2 gives
a poor fit; 3 and up gives a good fit. But now increase sigma to
0.5, say; fitting with degree 3 or 4 still gives o.k. results, but if
you increase the degree to 8, say, you see you that results
deteriorate. The model is then too flexible, and so it pays too much
attention to the spurious detail in the noisy data: it over-fits.
; rand generates a vector of random variables, all
uniformly distributed between 0 and 1. You'll see that degree 2 gives
a poor fit; 3 and up gives a good fit. But now increase sigma to
0.5, say; fitting with degree 3 or 4 still gives o.k. results, but if
you increase the degree to 8, say, you see you that results
deteriorate. The model is then too flexible, and so it pays too much
attention to the spurious detail in the noisy data: it over-fits.


Next: Writing up and presenting
Up: Research Methods
Previous: Accessing research literature
Sollich
2017-11-23
![]() /Documents/.
/Documents/.