ECONOPHYSICS

The lives of most of us depend on the dynamics of financial markets that affects investments, savings, business, employment, growth, wealth and -ultimately- the daily functioning of our society. Understanding, monitoring and managing the dynamics of financial markets is of crucial importance to policy-makers, financial institutions and businesses that are increasingly faced with managing risk, planning strategies and taking decisions in an increasingly complex market-place.

We are developing innovative, flexible methods to characterize, survey and monitor the financial market structure and the emergence of organized behaviours. The project involves the application of advanced ideas from statistical physiscs, mathematical finance, complex system studies and science of networks.

Our general aim is to contribute to the understanding of the fundamental aspects of the science of complex systems. Specific goals concern the development of tools to analyse the collective behaviour of complex systems such as financial markets, to understand their structure, to manage and control risk.

See article on ANU reporter

See research Highlights

Starting from correlation matrices we developed a new technique to construct networks containing the most relevant information.
Such a technique starts from the complete weighted graph Knrepresenting the correlations between nelements and extracts a significant sub-graph with constrained genus g.
Larger is the genus and larger is the amount of information retained in the sub graph up to the limit when the genus is above or equal to

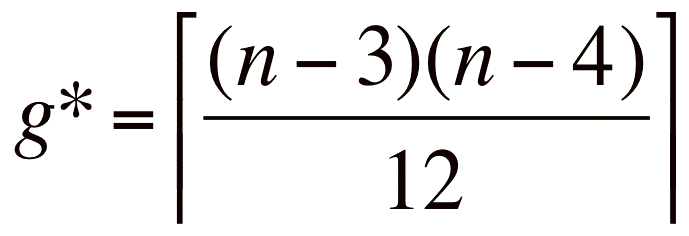
when the complete graph can be reconstructed.
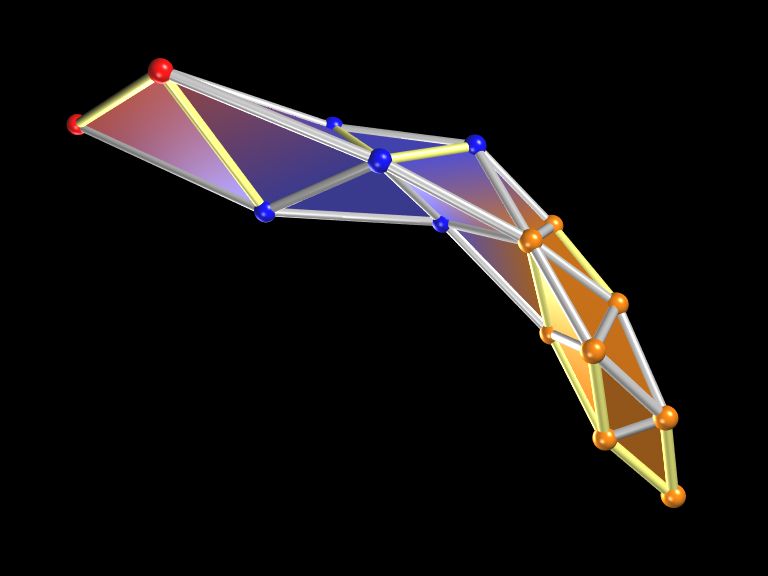
The simplest class of graphs is constructed in the case g=0which lead to a reticulation of a topological sphere.
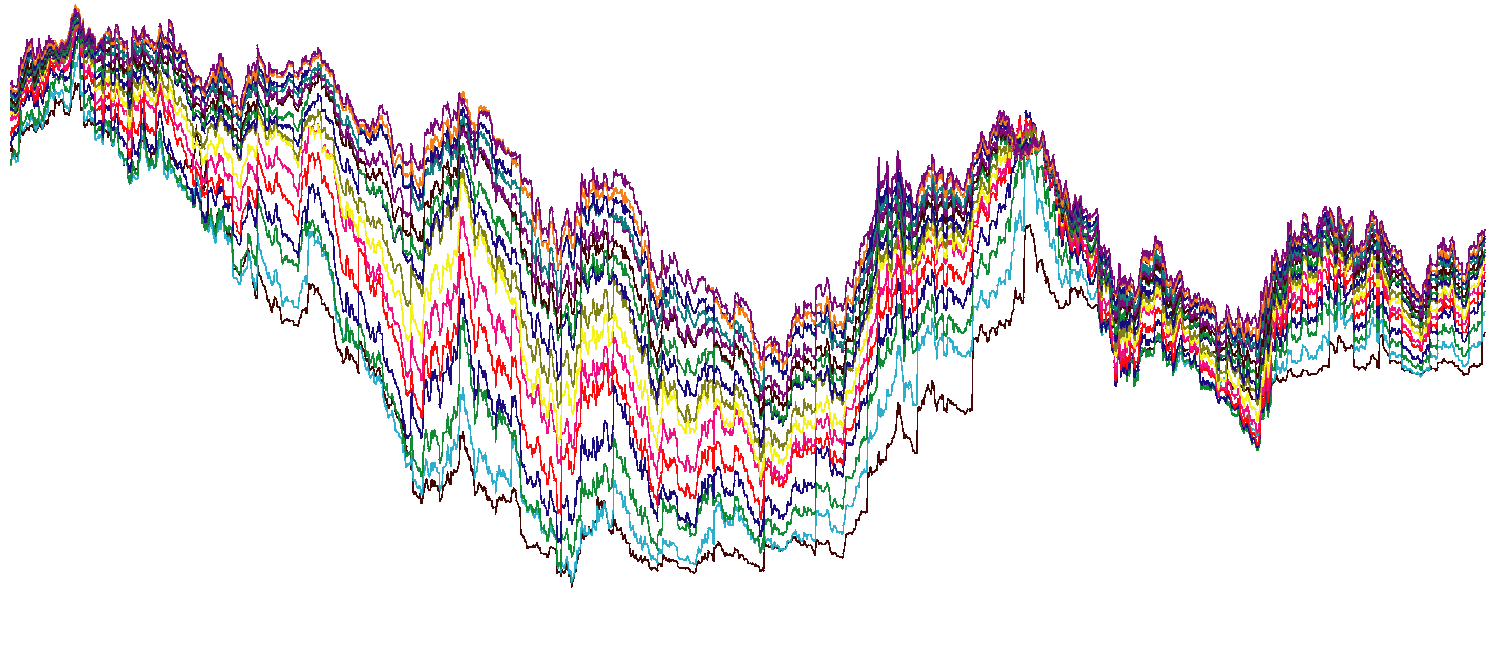
This technique is described in some detail in:   T. Di Matteo, T. Aste, S. T. Hyde and S. Ramsden, "Interest rates hierarchical structure", Physica A 355 (2005) 21-33; where a practical application to interest rates is also discussed. The resulting topological structures are shown hereafter in the case of Interest rates.

A more general discussion of this tecnique and its application to 100 stocks on a US equity market is presented in: M. Tumminello, T. Aste, T. Di Matteo, R. N. Mantegna, "A tool for filtering information in complex systems", Proceedings of the National Academy of Sciences of the United States of America Vol. 102, Num. 30 (2005) 10421-10426.
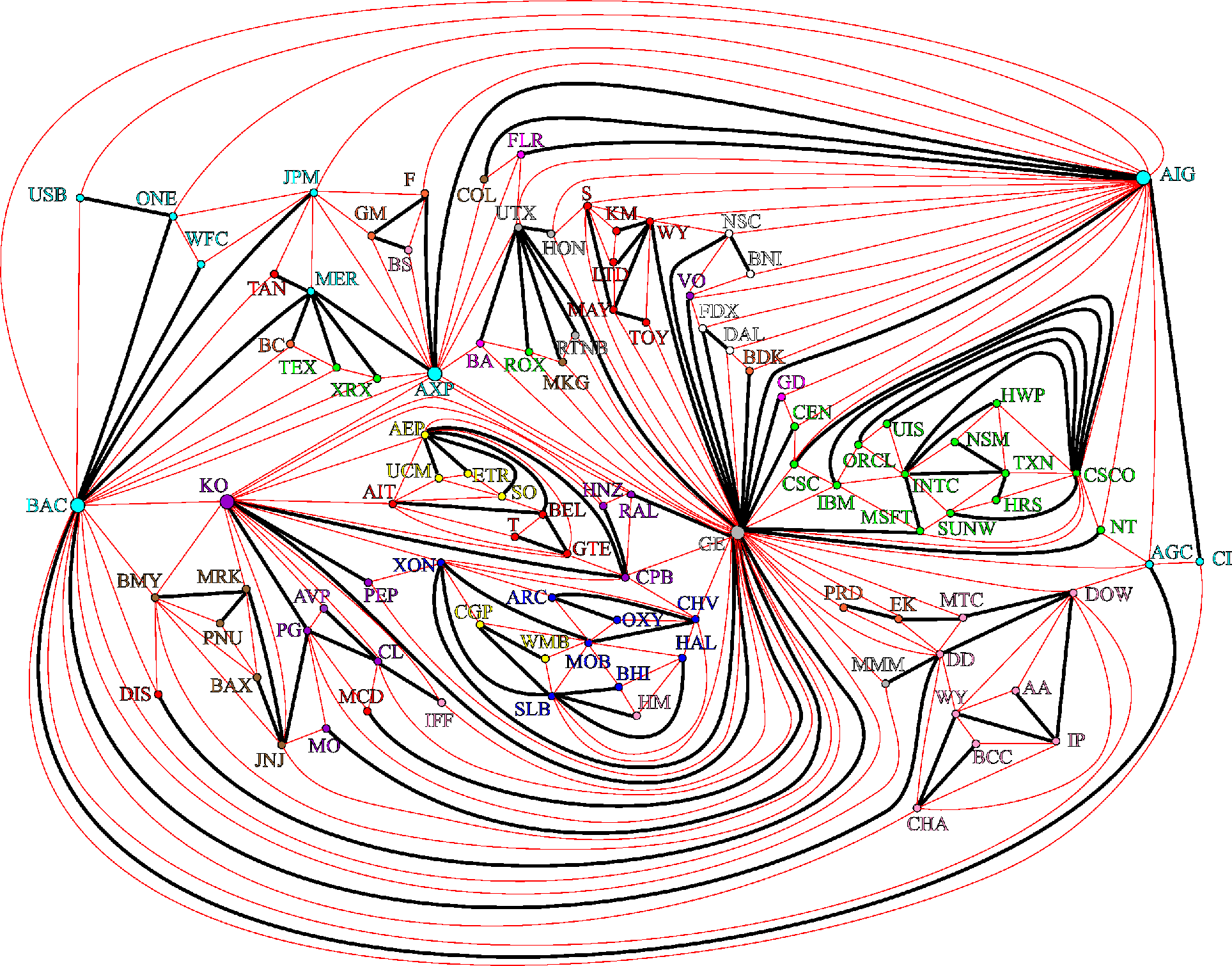
The planar graph resulting from the mapping of the correlation matrix onto a topological sphere is shown here below.

We study the topological properties of graphs embedded on manifolds with different genus.
We analyze the relation between the average genus per node and the network- topological structure highlighting the effect of local an global properties on the system of topological distances between  nodes.

It has been widely noted that complex interconnected structures appear in a wide variety of systems of high technological and intellectual importance. It has been pointed out that many such networks are disordered but not completely random. On the contrary, they have intrinsic hierarchies and characteristic organizations which are distinguishable and are preserved during the network evolution. In particular, one of the principal feature of these networks is the fact that they are both clustered and connected. For instance, an individual in a social network has most links within his own local circle, yet each individual in the world is only at a fewsteps from any other. An example of a completely clustered network is a triangular lattice on a planar surface: in such a network each one of the n nodes is connected with its local neighbors only and the average distance between two individuals scales as n0.5. This is a ‘large world’. On the other hand,  we know that random graphs are closely connected systems where the average distance scales as ln(n): a ‘small world’.
Intermediate structures can be constructed from the planar lattice by adding links between distant nodes making in this way short cuts. But such an insertion of a short-cut on the triangular lattice has an important consequence: the network can no longer be drawn on the plane without edge crossings; it is non-planar. The embedding surface must be modified accordingly by creating a ‘worm hole’ which connects two distant parts of the surface and through which the new link can ‘travel’. Such ‘worm holes’ create short-cut tunnels in the (2D) universe transforming it into a small world.

InT. Aste, T. Di Matteo, S. T. Hyde, "Complex networks on hyperbolic surfaces", Physica A 346 (2005) 20-26 (cond-mat/0408443)we explore the idea of a network that exists, grows and evolves on an hyperbolic surfacewith fixed genus. The complexity of the network itself is in this way associated with the complexity of the surface and the evolution of the network is now constrained to a given overall topological organization.
More precisely, we explore the relation between the properties of a network and its embedding on a surface.
An orientable surface can be topologically classified in term of its genuswhich is the largest number of non-intersecting simple closed cuts that can be made on the surface without disconnecting a portion (equal to the number of handles in the surface).
The genus (g) is a good measure of complexity for a surface: under such a classification, the sphere (g = 0) is the simplest system; the torus is the second-simpler (g = 1); etc. To a given network can always be assigned a genus.
Our approach works in two ways: it is a convenient tool to generate graphs with given complexity (genus) and/or it is a useful instrument to measure the complexity of real-world graphs.