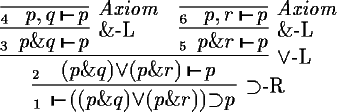
Jump to the implementation.
It is not very complicated to implement an interpreter for G4ip using a logic programming language (backtracking is directly supported within the language). Our first implementation is written in the logic programming language Lambda Prolog and can be found here. Another implementation by Hodas and Miller written in Lolli can be found here (see [Hodas and Miller, 1994]). These are simple and straightforward implementations of G4ip's rules. On the other hand it seems that imperative languages need a rather high overhead of code when implementing a logic calculus. For example choice points are usually implemented with stacks. We shall demonstrate the implementation technique of success continuations which provides an equally simple method for implementing logic calculi in imperative languages. This technique is not new: it has been introduced in [Carlsson, 1984]. This paper presents a rather technical implementation of Prolog in LISP. Later an excellent paper, [Elliot and Pfenning, 1991], appeared which describes a full-fledged implementation of Lambda Prolog in SML. We demonstrate the technique of success continuations for G4ip in Pizza.
Pizza is an object-oriented programming language and an attractive extension of Java. Although Pizza is a superset of Java, Pizza programs can be translated into Java or compiled into ordinary Java Byte Code (see [Odersky and Wadler, 1997] for a technical introduction to Pizza). We make use of the following two new features of Pizza:
F ::= false | A | F & F | F v F | F -> F
The class cases allow a straightforward implementation of this specification; it is analogous to the SML implementation of Lambda Prolog's formulae in [Elliot and Pfenning, 1991]. The class of formulae for G4ip is given below:
Two examples that illustrate the use of the representation are as follows:
p -> p
is represented as Imp(Atm("p"),Atm("p"))
a v (a -> false) is represented as Or(Atm("a"),Imp(Atm("a"),False()))
The class cases of Pizza also support an implementation of formulae specified by a mutually recursive grammar. This is required, for example, when implementing hereditary Harrop formulae.
The sequents of G4ip, which have the form Gamma=>G, are represented
by means of the class below. The left-hand side of each sequent is specified by a multiset
of formulae. Therefore, we do not need to worry about the order in which the
formulae occur.
We have a constructor for generating new sequents during proof search.
Context is a class which represents multisets; it is a simple
extension of the class Vector available in the Java libraries.
This class provides methods for adding elements to a multiset (add),
taking out elements from a multiset (removeElement) and testing
the membership of an element in a multiset (includes).
prove is the sequent being
proved; the second argument is an anonymous function. The function prove is now
of the form prove(sequent,sc). Somewhat simplified the
first argument is the leftmost premise and the second argument sc,
the success continuation, represents the other proof obligations. In case we
succeed in proving the first premise we then can attempt to prove the other
premises. The technique of success continuations will be explained using the following
proof (each sequent is marked with a number):
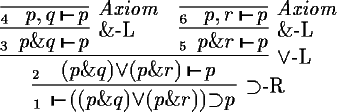
The inference rules fall into three groups:
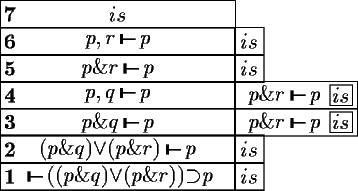
Suppose we have called prove with a sequent s and a
success continuation is. The inference rules of the first
group manipulate s obtaining s' and call prove
again with the new sequent s' and the current success continuation
(Steps 1-2, 3-4 and 5-6). The inference rules
of the second group have two premises, s1 and s2.
These rules call prove with s1 and a new success
continuation prove(s2,is) (Step 2-3).
The third group of inference rules only invoke the success continuation
if the rule was applicable (Steps 4-5 and 6-7).
We are going to give a detailed description of the code for the rules: &_L,
->_R, v_Ri, v_L and Axiom. The function prove receives as arguments
a sequent Sequent(Gamma,G) and a success continuation
sc. It enumerates all formulae as being principal and
two switch statements select a corresponding case depending on the form
and the occurrence of the principal formula.
The &_L rule is in the first group; it modifies the sequent being proved and calls
prove again with the current success continuation sc. The code is as
follows (Gamma stands for the set of formulae on the left-hand
side of a sequent excluding the principal formula; G stands
for the goal formula of a sequent; B and C stand
for the two components of the principal formula).
The code for the ->_R rule is similar:
The v_Ri rule is an exception in the first group. It breaks up a goal
formula of the form B1 v B2 and proceeds with one of its component.
Since we do not know in advance which component leads to a successful proof we have
to try both. Therefore this rule acts as a choice point, which is encoded by a
recursive call of prove for each case.
The v_L rule falls into the second group where the current success
continuation, sc, is modified. It calls prove with the first premise,
B,Gamma=>G, and wraps up the success continuation with the
new proof obligation, C,Gamma=>G. The construction
fun()->void {...} defines an anonymous function: the new
success continuation. In case the sequent B,Gamma=>G can be
proved, this function is invoked.
The Axiom rule falls into the third group. It first checks if the
principal formula (which is an atom) matches with the goal formula and
then invokes the success continuation sc in order to prove all remaining
proof obligations.
The proof search is started with an initial success continuation is.
This initial success continuation is invoked when a proof has been found.
In this case we want to give some response to the user, an
example for the initial success continuation could be as follows:
Suppose we attempt to start the proof search with prove(p,p => p,is).
We would find that the prover responds twice with "Provable!", because
it finds two proofs. In our implementation this problem is avoided by encoding
the proof search as a thread. Whenever a proof is found, the initial success
continuation displays the proof and suspends the thread. The user can
decide to resume with the proof search or abandon the search.
We had to make some compromises in order to support as many platforms as possible. This should change with the release of new browsers and a stable Java-specification (resp. Pizza-specification).
A paper about the implementation appeared in the LNAI series No 1397, Automated Reasoning with Analytic Tableaux and Related Methods, ed. Harry de Swart, International Conference Tableaux'98 in Oisterwijk, The Netherlands. The title is: Implementation of Proof Search in the Imperative Programming Language Pizza (pp. 313-319). The paper can be found here: DVI, Postscript (© Springer-Verlag LNCS).
Acknowledgements: I am very grateful for Dr Roy Dyckhoff's constant encouragement and many comments on my work. I thank Dr Gavin Bierman who helped me to test the prover applet.
Prover Applet
Jar Version
(slightly faster, but requires Netscape 4 or MS Explorer 4).
Last modified: Sun Sep 23 12:04:47 BST 2001